Lebesgue integral, Radon-Nikodym, Mutual Information and relative measurability
This post continues the previous example. It adds in definitions and terms relating to Lebesgue integrals and entropy.
Intro - Relative uncertanity
In the previous post I explored \(\sigma\)-algebras as a concept of “resolution” - the ability to classify outcomes of a random trial into various events. In some \(\sigma\)-algebras two outcomes may be considered the same event (c.f. \(X(\omega')=X(\omega)=B\)), but in another algebra, they can be considered two disctinct events (c.f. \(Z(\omega)=B\) vs \(Z(\omega')=C\)).
But it is very much natural to consider two random variables on the same set, but with various levels of uncertanity. If we forget about the interpretation for a moment, \(P_X\) and \(P_Y\) are probability measures with the same support but they have different levels of uncertanity associated with them. It is easier to predict the future value of \(X\) than the future value of \(Y\)
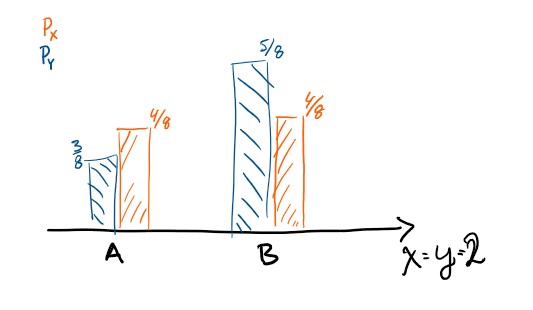
Using the probability of events as a measure of “relative certanity” instead of using filtrations can therefore describe richer nuance, and this post does this via entropy and mutual information after developing the lebesgue integral.
Relative uncertanity continued
One of the outcomes after last post was the measurable space \((\mathbb 2, \mathfrak P(\mathbb 2))\) and two different probability measures, called \(P_X\) and \(P_Y\). We also had a second measurable space \((\mathbb 3, \mathfrak P(\mathbb 3))\) with the probability measures \(P_Z\). It is also possible to consider \(P_X,P_Y\) as functions on \((\mathbb 3, \mathfrak P(\mathbb 3))\) as well, which we will do.
The measures are uniquely determined by their values on the elementary events, so we can iterate them here below. In the table, I also include the uniform probability measure, which I will call \(P_u\). I also add the counting measure \(\#\), which is not a probability measure. It is the cardinality on finite sets, otherwise it is infinite.
| elementary event \(\mathcal A\) | \(P_X(\mathcal A)\) | \(P_Y(\mathcal A)\) | \(P_Z(\mathcal A)\) | \(P_u(\mathcal A)\) | \(\#(\mathcal A)\) |
|---|---|---|---|---|---|
| \(\{A\}\) | \(4/8\) | \(3/8\) | \(4/8\) | \(1/3\) | \(1\) |
| \(\{B\}\) | \(4/8\) | \(5/8\) | \(2/8\) | \(1/3\) | \(1\) |
| \(\{C\}\) | \(0\) | \(0\) | \(2/8\) | \(1/3\) | \(1\) |
The lebesgue integral for nonnegative functions
This presentation is a copy of the presentation in Wikiepdia, and verified against Rudins Principles of Mathematical Analysis.
Define a function called an indicator function1 on a set \(1_A: \Omega \to \{0,1\}\) to be
\[1_A(x) = \begin{cases} 1 &\text{if } x \in A \\ 0&\text{else} \end{cases}\]Define the lebesgue integral of the indicator function over a measure space \((\Omega,\mathcal F,\mu)\) to be 2
\[\int 1_A d\mu = \mu(A)\]Integration should always be linear, so we can naturally extend the definition to finite linear combinations of disjoint sets. Let \(f_s = \sum_ka_k1_{S_k}\) where \(a_k \in \{r :r\in\mathbb R, r\geq 0\}\) and \(S_i \cap S_j = \emptyset\) for all \(i\neq j\). Such functions are called simple functions.
\[\int f_s d\mu = \sum_k a_k \mu(S_k)\]Any function can be approximated arbitratily well by simple functions. We need to assume \(\mu(S_k) < \infty\) if \(a_k \neq 0\) to avoid some pathological cases.
The integral over some measurable set \(B\) is defined quite naturally
\[\int_Bf_s d\mu = \sum_k a_k \mu(S_k\cap B)\]Define the lebesgue integral of a non-negative function \(f^+\) to be
\[\int_B f^{+} d\mu = \sup_{\{f_s: 0\leq f_s(x) \leq f(x) ,\, f_s \text{ simple}\}} \int_B f_s d\mu\]For any real function, we decompose it into a nonnegative \(f^+\) and a nonpositive part \(-f^-\), we define the lebesgue integral to be
\[\int_B f d\mu = \int_B f^+d\mu - \int_B f^- d\mu\]A very important special case pops out directly. If you have a function \(f:\Omega\to \mathbb R\), \(\Omega\) is finite and equiped with the counting measure \(\#\) (implies powerset \(\sigma\)-algebra) then
\[\int_\Omega f d\# = \sum_{k\in\Omega}f(k)\]Change of variables - Radon-Nikodym
Consider a measurable space \((\Omega,\mathcal F)\), and two measures \(\mu\) and \(\nu\) defined on \(\mathcal F\). We say \(\mu \ll \nu\), that \(\mu\) is absolutely continous with respect to \(\nu\) if and only if \(\nu(A)=0\) implies \(\mu(A)=0\). A synonym is that \(\nu\) dominates \(\mu\). 3
One can verify that \(P_X \ll P_Z\) in the example, but the converse does not hold. Also, \(P_X \ll P_u\)
Consider a measure space \((\Omega,\mathcal F,\mu)\). If you can construct a countable collection of measurable sets \(\{\mathcal A_k\}_{k=1}^{\infty}\) so that \(\mu(\mathcal A_k)<\infty\) for all \(k\), and that \(\bigcup_{k=1}^{\infty}\mathcal A_k = \Omega\), we say that \(\mu\) is a \(\sigma\)-finite measure over \((\Omega,\mathcal F)\).
For a finite set \(\Omega\), any finite measure is \(\sigma\)-finite. This applies to our running example, since \(\mathbb 3\) is finite, and all probability measures (includeing \(P_X,P_Y,P_Z\)) are finite measures.
The Radon-Nikodym theorem says that if \(\nu \ll \mu\) and both are \(\sigma\)-finite over \((\Omega,\mathcal F)\), there exists a nonnegative \(\mathcal F\)-measurable function called the Radon-Nikodym derivative, notated like \(\frac{d\nu}{d\mu}\). It is uniquely defined almost everywhere. It has the property that
\[\int_A \frac{d\nu}{d\mu} d\mu = \int_A d\nu = \nu(A)\]This also implies the change-of-variables formula
\[\int_A f \frac{d\nu}{d\mu} d\mu = \int_A f d\nu\]and the chain rule
\[\pi \ll \nu \ll \mu \Rightarrow \frac{d\pi}{d\nu} \frac{d\nu}{d\mu} = \frac{d\pi}{d\mu}\]and inversion
\[(\nu \ll \mu) \text{ and } (\mu \ll \nu) \Rightarrow \left(\frac{d\mu}{d\nu}\right)^{-1} = \frac{d\nu}{d\mu}\]In our concrete example, the Radon Nikodym derivatieves can be computed easily by working with the elementary events. We work through an example that can be extended simply.
\[P_X(\mathcal A) = \int_{\mathcal A}\frac{dP_X}{dP_u} P_u\]Choose \(\mathcal A = \{k\}\), i.e. an elementary event.
\[P_X(\{k\}) = \int_{\{k\}}\frac{dP_X}{dP_u} P_u\]Next, decompose the derivative into a linear combination of indicators. The decomposition must be finite, since we work with a finite sample space \(\mathbb 3\).
\[P_X(\{k\}) = \int_{\{k\}}\sum_{j\in \mathbb 3} \frac{dP_X}{dP_u}(j)1_{\{j\}} P_u\]By linearity we get
\[P_X(\{k\}) = \sum_{j\in \mathbb 3} \frac{dP_X}{dP_u}(k)P_u(\{k\}\cap \{j\}) = \frac{dP_X}{dP_u}(k)P_u(\{k\})\]or in conclusion
\[\frac{dP_X}{dP_u}(k) = \frac{P_X(\{k\})}{P_u(\{k\})}\]We can, in the same way, derive \(\frac{dP_X}{d\#}(k) = P_X(\{k\}) =: p_X(k)\). This function is very special, and we call it the probability function for a discrete variable. I should mention, though, that there are myriads of other ways to motivate the probability function than the Radon-Nikodym derivative.
What is nice with this construction is that it also works well with other spaces and measures. If \(P_X\) is a probability measure over the real line, and \(\lambda\) is the lebesgue measure, then \(\frac{dP_X}{d\lambda}\) is the density of \(X\). The choice of \(\lambda\) is as natural to us as a standard measure of ‘size’ of segments of the real line as counting members in a finite set. See some discussion here or more rigorously here
Entropy
Define the Relative Entropy4 between two measures \(P\) and \(Q\) so that \(P\ll Q\)over some common measurable space \((\Omega,\mathcal F)\) to be
\[D_{KL}(P\|Q) := \int_\Omega \frac{dP}{dQ} \log \left(\frac{dP}{dQ}\right) dQ\]This may look like an abstract mess, but think of it as something nicely abstractly defined that just so happens to have special cases that fall out in a nice way for us. Notable features are that it is nonnegative, has a global minimum \(P=Q\),
If I choose \(Q=\#\) then this boils down into
\[\begin{aligned} D_{KL}(P\| \#) &= \int_\Omega \frac{dP}{d\#} \log \left(\frac{dP}{d\#}\right) d\# \\ &= \int_\Omega p \log p d\# \\ &= \sum_{k\in\Omega} p(k) \log p(k) \end{aligned}\]This is called the negative entropy of a discrete random variable, and with a change of sign, we get back the commonly defined entropy
\[H(P) := - \sum_{k\in\Omega}p(k)\log p(k)\]I think of this as the relative entropy between the counting measure and the probability measure in question. Choosing the \(Q\) to be the lebesgue measure we obtain the negative differential entropy that we would hope for.
I would also like to mention that often uses the 2-logarithm and calls the unit of measurement bit or shannon. One could as well use log-e and call the unit nat.
In this way, we may compute some various entropies. Notice that since \(\#\) is not a probability measure it has entropy \(0\). That is not possible for probability measures.
| \(P\) | \(H(P)\) [bits] |
|---|---|
| \(P_X\) | \(1\) |
| \(P_Y\) | \(0.954\) |
| \(P_Z\) | \(1.5\) |
| \(P_u\) | \(1.585...\) |
| \(\#\) | \(0\) |
From this, we can see that the entropy is the lowest for \(Y\), and that is the distribution that is the most certain (one outcome is much more probable thasn the others). But this certanity measure is only against the counting measure. Now, can we say something about the uncertanity for a relation between two random variables directly?
Joint random elements
Step one is to introduce product random elements. Take a finite number of random elements \(\{W_i\}_{i=1}^n\) so that \(W_i: (\Omega , \mathcal F) \to (\mathcal W_i,\mathcal E_i)\) are measurable functions. Using the normal cartesian product \(\prod_{i=1}^{n}\mathcal W_i\) is a set, and \(\prod_{i=1}^{n}\mathcal E_i =: \mathcal E\) is a \(\sigma\)-algebra on that set. It is simple to define a new random element \(W\) according to
\[W: (\Omega , \mathcal F) \to (\mathcal W,\mathcal E)\] \[W: \omega \mapsto (W_1(\omega),...W_n(\omega)\]We also use the notation \(W=(W_1,W_2,...W_n)\).
By this definition, we may consider the random element \((X,Y,Z)\) and analyze its pushforward measure over \(\mathcal X \times \mathcal Y \times \mathcal Z = \mathbb 2 \times \mathbb 2 \times \mathbb 3\). Lets tabulate the pushforward measure, and compare with the counting measure! As a computation example consider the follwoing.
\[\begin{aligned} &P\sharp (X,Y,Z)((\{B\},\{A\},\{C\})) = \\ & P((X,Y,Z)^{-1}((\{B\},\{A\},\{C\}))) = \\ & P(X^{-1}(\{B\}) \cap Y^{-1}(\{A\}) \cap Z^{-1}(\{C\})) = \\ & P( \{C,D,E,F\} \cap \{A,C,E\} \cap \{E,F \}) = \\ & P(\{E\}) = \\ & 1/8 \end{aligned}\]In this fashion, we may continue to compute the full measure.
| \(\mathcal A\) | \((X,Y,Z)^{-1}(\mathcal A)\) | \(P_{(X,Y,Z)}(\mathcal A)=P\sharp (X,Y,Z)(\mathcal A)\) | \(\# (\mathcal A)\) |
| \((\{A\},\{A\},\{A\})\) | \(\{A\}\) | \(1/8\) | \(1\) |
| \((\{A\},\{A\},\{B\})\) | \(\emptyset\) | \(0\) | \(1\) |
| \((\{A\},\{A\},\{C\})\) | \(\emptyset\) | \(0\) | \(1\) |
| \((\{A\},\{B\},\{A\})\) | \(\{B\}\) | \(3/8\) | \(1\) |
| \((\{A\},\{B\},\{B\})\) | \(\emptyset\) | \(0\) | \(1\) |
| \((\{A\},\{B\},\{C\})\) | \(\emptyset\) | \(0\) | \(1\) |
| \((\{B\},\{A\},\{A\})\) | \(\emptyset\) | \(0\) | \(1\) |
| \((\{B\},\{A\},\{B\})\) | \(\{C\}\) | \(1/8\) | \(1\) |
| \((\{B\},\{A\},\{C\})\) | \(\{D\}\) | \(1/8\) | \(1\) |
| \((\{B\},\{B\},\{A\})\) | \(\emptyset\) | \(0\) | \(1\) |
| \((\{B\},\{B\},\{B\})\) | \(\{E\}\) | \(1/8\) | \(1\) |
| \((\{B\},\{B\},\{C\})\) | \(\{F\}\) | \(1/8\) | \(1\) |
Marginals and the mutual information
Consider the random element \((X,Y)\) constructed like above. It has a measure \(P_{X,Y}\). The non-joint pushforward measures \(P_{X}\) and \(P_{Y}\) are called the marginal probabilities.
For some event \(A \in \mathcal X\) and some event \(B \in \mathcal Y\), we can define the product measure \(P_{X \otimes Y}(A,B) = P_X(A)P_Y(B)\). The product measure considers \(X\) and \(Y\) to be independent, but the joint probability also captures how they co-vary.
The mutual information between two random elements is the KL distance between their joint and their product.
\[I(X;Y) := D_{KL}(P_{X,Y}\|P_X \otimes P_Y)\]The relation between entropy and \(\sigma\)-algebra
Entropy for a random element on a finite range is defined as the negative KL distance from the counting measure to the pushforward measure.
\[H(P_X) = D_{KL}(P_X\|\#)\]In that case, \(I(X;X) = H(P_X)\)
Consider a random element \(X\) with finite range \(\mathcal X\), pushforward measure \(P_X\), and the uniform measure \(u\), and the counting measure \(\#\) over \(\mathcal X\). Let \(p_X\) and \(p_u\) be their respective probability functions. Notice \(p_u(x)=1/\#(\mathcal X)\) always.
The information inequality, also called Gibbs’ inequality, states that \(0 \leq D_{KL}(P\| Q)\) for all measures \(P\) and \(Q\), so
\[\begin{aligned} 0 \leq D_{KL}(P_X\| u) &= \int_{\mathcal X} \frac{dP_X}{du} \log \left(\frac{dP_X}{du}\right) du \\ &= \int_{\mathcal X} \frac{dP_X}{d\#}\left(\frac{du}{d\#} \right)^{-1} \log \left(\frac{dP_X}{d\#}\left(\frac{du}{d\#} \right)^{-1}\right) \frac{du}{d\#} d\# \\ &= \sum_{x\in{\mathcal X}} p_x(x) \log \frac{p_X(x)}{p_u(x)} \\ &= \sum_{x\in{\mathcal X}} p_x(x) \log \frac{p_X(x)}{p_u(x)} \\ &= \sum_{x\in{\mathcal X}} p_x(x) \log \frac{1}{p_u(x)} - H(P_X)\\ &= \sum_{x\in{\mathcal X}} p_x(x) \log \#(\mathcal X) - H(P_X)\\ &= \log \#(\mathcal X) - H(P_X) \end{aligned}\]implying that \(H(P_X) \geq \log \#(\mathcal X)\). The log-cardinality of the range of a random variable thus sets a upper bound on the
In the running example, \(\sigma(X) \subset \sigma(Z)\), implying that \(\#(\mathcal X) < \#(\mathcal Z)\). The worst possible entropy \(Z\) could have is higher than the worst possible entropy of \(X\).
Furthermore, since \(\sigma(X) \subset \sigma(Z)\), or \(X \in \sigma(Z)\), we know there is an almost everywhere uniquely defined measurable function \(g: x \mapsto z\) so that \(P_X = P_Z \sharp g\) and \(X = g \circ Z\) almost everywhere. Since in our case, there are no sets of measure zero, that means everywhere.
If the function \(g\) is injective, one can show that \(H(P_Z) = H(P_X)\). But we know that it is not, and that implies (can be shown to imply) that \(H(P_Z) > H(P_X)\). This holds in the discrete case.
There is yet another result called the information processing inequality, which has the corollary that if \(\sigma(X) \subset \sigma(Z)\) implies \(I(Y;Z) \geq I(Y;X)\) if \(X=g(Z)\).
So the existance of a natural filtration implies bounds on the mutual information between random elements.
-
The indicator functions is called Characteristic functions in th field of analysis. See e.g. Principles of Mathematical Analysis by Walter Rudin [ISBN-10: 0-07-085613-3]](https://isbnsearch.org/isbn/0070856133) ↩
-
Of course, A has to be \(\mathcal F\)-measurable. I.e. \(A \in \mathcal F\). I.e. \(A\) has to be an event in the \(\sigma\)-algebra \(\mathcal F\). ↩
-
The notion of dominated measures is important if we ever want to consider expression in the style of \(\frac{\mu(A)}{\nu(A)}\). We then want \(\nu\) to dominate \(\mu\), since we don’t want to divide by zero. ↩
-
I choose to call it Relative Entropy, since it highlights how normal entropy falls out of it. It is often called Kullback-Liebler Divergence, which motivates its symbol and highlights its use as a distance measure / divergence. Its just a matter of convention… ↩
